Tasks
| |
Release two discs from opposite ends of the curve. Which disc will reach the bottom first? |
| |
Try again, but release the discs from different positions. Which disc will win the race this time? |
| |
Can you think of any applications for this special curve? |
|
Maths
The two discs always reach the bottom of the curve at the same time – no matter where you release the discs. This type of curve is called a tautochrone, “tauto-” means “same” and “-chrone” means time.
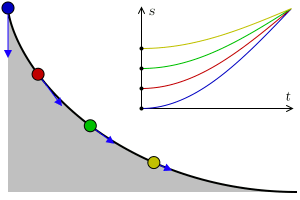
If a disc has twice the distance to travel, it must start with twice the acceleration (due to gravity) to reach the end at the same time. Working out which curve has this property is a difficult problem.
One solution is the curve drawn by a point on the rim of a wheel as it rolls along the ground. This is curve called a cycloid.
 The time it takes to reach the end is equal to the time it takes an object to fall vertically from a height of 2r, where r is the radius of the circle that generates the cycloid. The time it takes to reach the end is equal to the time it takes an object to fall vertically from a height of 2r, where r is the radius of the circle that generates the cycloid.
|
History
In 1602, Italian scientist Galileo Galilei conceived of the idea for using pendulums for time-keeping. However, if two pendulums are released from different heights they slowly move out of synch. A free pendulum follows a circular path, so mathematicians began to wonder whether there was another curve for a pendulum that keeps the same time no matter where it is released.
Dutch mathematician Christiaan Huygens solved the problem in 1659. Huygens’s solution was a cycloid. If a pendulum follows a cycloid path (shown above) instead of a circular path, its timing is always the same. Unfortunately, real-life cycloid pendulums lose time due to friction, so they are impractical for actual time-keeping.
|
People
 Galileo Galilei 1564 – 1642 Galileo Galilei 1564 – 1642
Galileo was an Italian astronomer, physicist, and engineer. Galileo was the first to consider using a pendulum for keeping time. Galileo also investigated the mathematics of the cycloid, but did not connect that a cycloid pendulum always keeps the same time. |
 Christiaan Huygens 1629 – 1695 Christiaan Huygens 1629 – 1695
Huygens was a mathematician and physicist who was one of the first to use mathematical formulas to describe the laws of physics. Huygens invented the pendulum clock which became the most accurate timekeeper for 300 years. Huygens solved the path a pendulum needs to make to always keep the same time, called the tautochrone. |
|
Applications
The time-keeping property of the cycloid was discovered while trying to design better clocks. Unfortunately, the cycloid pendulum introduces more errors than it fixes, so the design was abandoned. But it is an example of how real-life problems can lead to interesting mathematical discoveries.
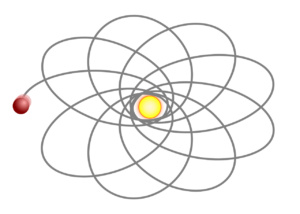
A cycloid is the curve traced by a circle as it rolls along a straight line. The idea is similar to a spirograph, the toy that creates beautiful spiral patterns by rolling a circle inside other circles. The cycloid and spirographs are both examples of roulettes. In astronomy, some objects can have complex orbits similar to the patterns created by roulettes.
|
Maths at Home
The curve used in this activity is called a cycloid. A cycloid is the curve drawn by a point of the rim of a wheel as it rolls along the ground. If we roll a circle inside another circle we get spirals. These are the same kinds of patterns made by a Spirograph. Try this online Spirograph (called Inspirograph) and see what kind of patterns you can make,
Can you make a cycloid? What do you need to make a cycloid?
|






