Atmospheric Turbulence

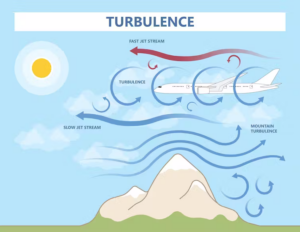
Turbulence is caused by wind passing over obstacles such as mountains, or winds of different speeds and temperatures colliding.

Atmospheric turbulence causes unpredictable swirling patterns of all sizes. On a larger scale, hurricanes are caused by the rotation of the Earth itself.

Predicting turbulence is important to weather forecasting and air travel. Although we cannot predict individual pockets of turbulence, we can predict which conditions are likely to result in turbulence.

Turbulence is also an example of chaotic behaviour. This means that small changes in the atmosphere can result in very different patterns. This is sometimes called the butterfly effect, which is the idea that a butterfly flapping its wings could result in a tornado on the other side of the world.

Sometimes the changes can be so small that there is no way to measure them. This is one of the reasons why weather predications cannot be made beyond ten days.

Ancient weather forecasting was based on observation and pattern recognition. However, not all of these predictions were reliable.

Weather forecasting only became possible after the invention of telecommunications, which allowed weather reports to travel faster than weather itself. Later, computers made it possible to solve the complicated mathematical equations that describe the atmosphere.

In the 1960s, American mathematician Edward Lorenz noticed that small changes in weather simulations lead to very different results. This showed that even very precise measurements cannot be used to make long-term weather predictions.

Air turbulence is an important consideration to the design of cars and areoplanes. In fact, some turbulence is necessary to reduce the effect of drag.

For example, if a golf ball was smooth, air flowing over the ball would separate early, creating a region of of low pressure behind the ball, slowing it down. To prevent this, a golf ball is dimpled, creating turbulence, resulting in the air flow clinging to the ball for longer.

Weather forecasting uses observational data collected from weather stations around the world. Forecasts are computed using the mathematical equations for the physics and dynamics of the atmosphere. These equations are impossible to solve exactly, so numerical methods obtain approximate solutions.

In the future, Artificial Intelligence may be able to may forecasts purely from the data, without the need for physics based models.

A good way to experience air turbulence is to fly a kite. Instructions of how to make a kite can be found here.

Near the ground, the wind may swirl and gust because of turbulence caused by obstructions such as trees and buildings. These obstructions can cause turbulence as far downwind by as much as seven times the height of the obstruction.

Further away from the ground, the wind is fairly constant and parallel to the surface of the earth. However you may still experience sudden pockets of turbulence and unpredictable changes in direction.